
So, the triangle is not isosceles but equiangular. Solution: We observe that since all the angles measure 60circ. Triangle E is an obtuse triangle since it has an obtuse angle, while triangle F is an acute triangle since all its angles are acute. In an isosceles triangle, the equal sides measure 4 inches and all the angles measure 60circ. Furthermore, there can be at most one obtuse angle, and a right angle and an obtuse angle cannot occur in the same triangle. Proposition I.17 states that the sum of any two angles in a triangle is less than two right angles, therefore, no triangle can contain more than one right angle.
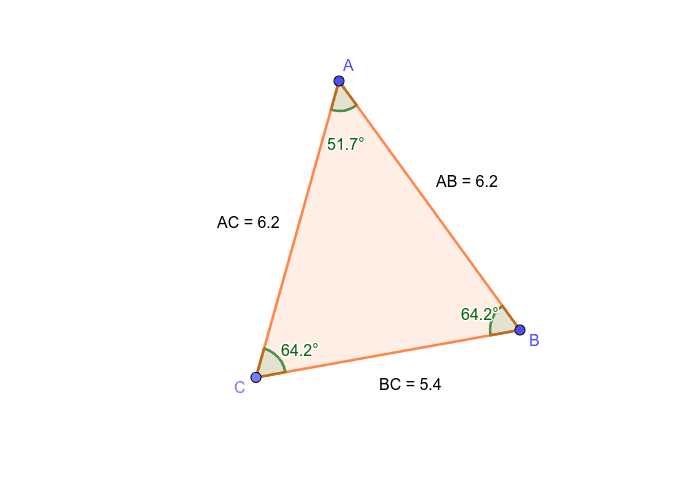
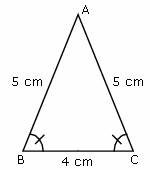
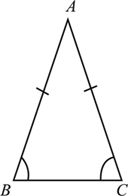
Since triangle D has a right angle, it is a right triangle. Before we dive into the in-depth definition, a scalene triangle is a triangle that has no equal sides. The triangle has two sides of length 5 and one side of length 8. An isosceles triangle is a triangle that has two equal sides and two equal angles. For example, consider an isosceles triangle ABC with two sides of length 5 and one side of length 8. An alternate characterization of isosceles triangles, namely that their base angles are equal, is demonstrated in propositions I.5 and I.6. A triangle is called an equilateral triangle if all three of its sides are equal and its angles are equal as well (60 each). Base Angles: The base angles of an isosceles triangle are the angles formed by the base and one leg of the triangle. The base of an isosceles triangle is the non-congruent side in the triangle. It is only required that at least two sides be equal in order for a triangle to be isosceles.Įquilateral triangles are constructed in the very first proposition of the Elements, I.1. Definition Base: The side of a triangle parallel with the bottom edge of the paper or screen is commonly called the base. The way that the term isosceles triangle is used in the Elements does not exclude equilateral triangles. The term isosceles triangle is first used in proposition I.5 and later in Books II and IV. (geometry) a flat shape with two of its three straight sides the same length. The equilateral triangle A not only has three bilateral symmetries, but also has 120°-rotational symmetries.Īccording to this definition, an equilateral triangle is not to be considered as an isosceles triangle. The scalene triangle C has no symmetries, but the isosceles triangle B has a bilateral symmetry. This definition classifies triangles by their symmetries, while definition 21 classifies them by the kinds of angles they contain. In contrast, triangles having same shape but of different size are called similar triangles.Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute-angled triangle that which has its three angles acute. Mathematically, triangles with same side length and angle measure are called congruent triangles. Congruent vs Similar TrianglesĪs we know, congruent triangles are triangles having the same shape and the same size. a triangle with two sides of equal length 3. a triangle with two sides of equal length 2. SSA Rule: If two corresponding sides and an angle are congruent, the said triangles may not be congruent as there are two different shapes possible for the triangle. isosceles triangle définition, signification, ce quest isosceles triangle: 1. Theorems Not Applicable to Prove Triangles CongruencyĪAA Rule: If all the corresponding angles of a triangle are congruent with the corresponding angles of another triangle, the triangles will be of the same shape but not necessarily of the same size. It states that if the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the two triangles are congruent.
5) Hypotenuse-Leg (HL) Rule of a Right Angle Theorem It states that if two angles and a non-included side of one triangle are congruent to two angles and a non-included side of another triangle, then the two triangles are congruent. It states that if two angles and the included side of one triangle are congruent to two angles and included side of another triangle, then the two triangles are congruent. It states that if two sides and the included angle of one triangle are congruent to two sides and included angle of another triangle, then the two triangles are congruent. It states that if three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent. Proving Triangles Congruence Rules Theorems 1) Side–Side-Side (SSS) Theorem isosceles triangle - a triangle with two equal sides triangle, trigon, trilateral - a three-sided polygon Based on WordNet 3.0, Farlex clipart.


 0 kommentar(er)
0 kommentar(er)
